 ОДУ
> Краевые задачи >
Разностные схемы
ОДУ
> Краевые задачи >
Разностные схемы
Разностные схемы для ОДУ
Разберем идею разностного метода решения краевых задач на
примере взаимодействия световых пучков, переобозначив в системе (О постановке-1 ) интенсивность излучения вправо на Y, а интенсивность
излучения влево на y (просто в целях удобства, чтобы не писать индекс). Суть
метода заключается в покрытии расчетного интервала сеткой из N точек. Тем самым
определяются (N-1) шагов (см. рис.). Затем надо заменить дифференциальные
уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных
разностях, выписав соответствующие разностные уравнения для каждого i-го шага. В
нашем случае достаточно просто заменить первые производные из (О постановке-1) их разностными аналогами (такой метод
называется еще методом
Эйлера):
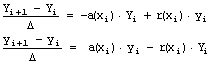 (1)
(1)
Замечание
Аппроксимировать дифференциальные
уравнения разностными можно множеством различных способов. От выбора конкретного
варианта зависит не только простота, быстрота и удобство вычислений, но и сама
возможность получения правильного ответа.
Получилась система (по числу шагов)
2(N-1) разностных линейных алгебраических уравнений с 2N неизвестными Yi и yi.
Для того, чтобы она имела единственное решение, надо дополнить число уравнений
до 2N. Это можно сделать, записав в разностном виде оба граничных
условия:
Y0=I0, yN=RYN. (2)
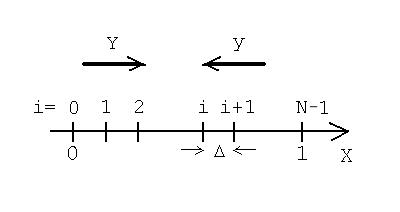
Рис. Сетка, покрывающая расчетный интервал
Сформированная полная система алгебраических
уравнений называется разностной схемой, аппроксимирующей исходную краевую
задачу. Обратите внимание, что правые части разностных уравнений системы (1) на
каждом шаге записаны для левой границы шага. Такие разностные схемы называют
явными, т. к. все значения Yi+1 и yi+1 находятся в левой части уравнений.
Полученную явную разностную схему легко записать в матричной
форме
Az=B, (3)
где z - неизвестный
вектор, получающийся объединением векторов Y и y. Решив систему (3), мы получим
решение краевой задачи.
Замечание
На самом деле, все несколько сложнее, поскольку, вообще
говоря, необходимо еще доказать, что, во-первых, разностная схема действительно
аппроксимирует дифференциальные уравнения и, во-вторых, при N, стремящемся к бесконечности, разностное
решение действительно сходится к дифференциальному.
Процесс решения системы разностных уравнений называют
также реализацией разностной схемы
 .
.
Дадим минимальные комментарии, надеясь, что заинтересовавшийся читатель с
карандашом в руках разберется в порядке индексов и соответствии матричных
элементов, а, возможно, составит и более удачную программу.
В первой строке листинга определяются функции и константы,
входящие в модель, во второй задается число точек сетки N=5 и ее равномерный шаг. Следующие две строки определяют матричные коэффициенты, аппроксимирующие
уравнения для Yi, а следующие две - для yi. Седьмая и восьмая строки листинга задают соответственно левое и правое граничное условие, а следующие три строки -
правые части системы (3). В следующей строке завершается построение матрицы A вырезанием из нее левого нулевого столбца. В предпоследней строке листинга
применена встроенная функция lsolve для решения
системы (3), а в последней выведены рассчитанные ею неизвестные граничные
значения. Графики решения приведены на рис. внизу, причем первые N элементов
итогового вектора есть вычисленное излучение вперед, а последние N элементов -
излучение назад.
Рис. Решение
краевой задачи разностным методом
Как мы увидели, реализация в Mathcad разностных схем вполне возможна и не слишком трудоемка - предложенная программа состоит всего из двух десятков математических выражений. Конечно, для их написания требуется и время, и часто кропотливые расчеты, но, собственно, в этом и состоит работа математика.